1.9

I wanted to get some experience with Blender’s simulation nodes capability in geometry nodes. This video is an exploration of simulating Newtonian gravity, but with a modification to the exponent. The implementation in Geometry Nodes also allows for dynamic movement of the central star, and adjustment of its mass.

At a high level, the video below was created with Blender Geometry Nodes simulation zone. The points are randomly generated on the surface of a cube at every frame. The points are given an initial velocity and the position and velocity is updated every frame according to the law of gravitation (more on this below). Each point is also colored according to its velocity where higher velocities are warmer (redder) colors, and slower velocities are cooler (bluer) colors. Finally, I can change key aspects of the simulation including the exponent used in the gravitation model. Changing this from 2 to 1.9 gives rise to the patterns in this video.

According to Newton’s law of gravitation, the attractive force between two massive bodies is given as:

\[F_G = \frac{Gm_1m_2}{r^2}\]

Where G is the gravitational constant: $G=6.67430(15)×10^{−11}$, $m_1$ and $m_2$ is the mass of the two bodies, and $r$ is the distance between the massive bodies.

With the introduction of simulation nodes in Blender, we have the ability to update a geometry once per frame according to any calculation that can be done in geometry nodes. Following loosely Simon Thommes Simulation Nodes Tutorial I implemented the geometry node graph below in order to implement Newton’s law of gravitation.

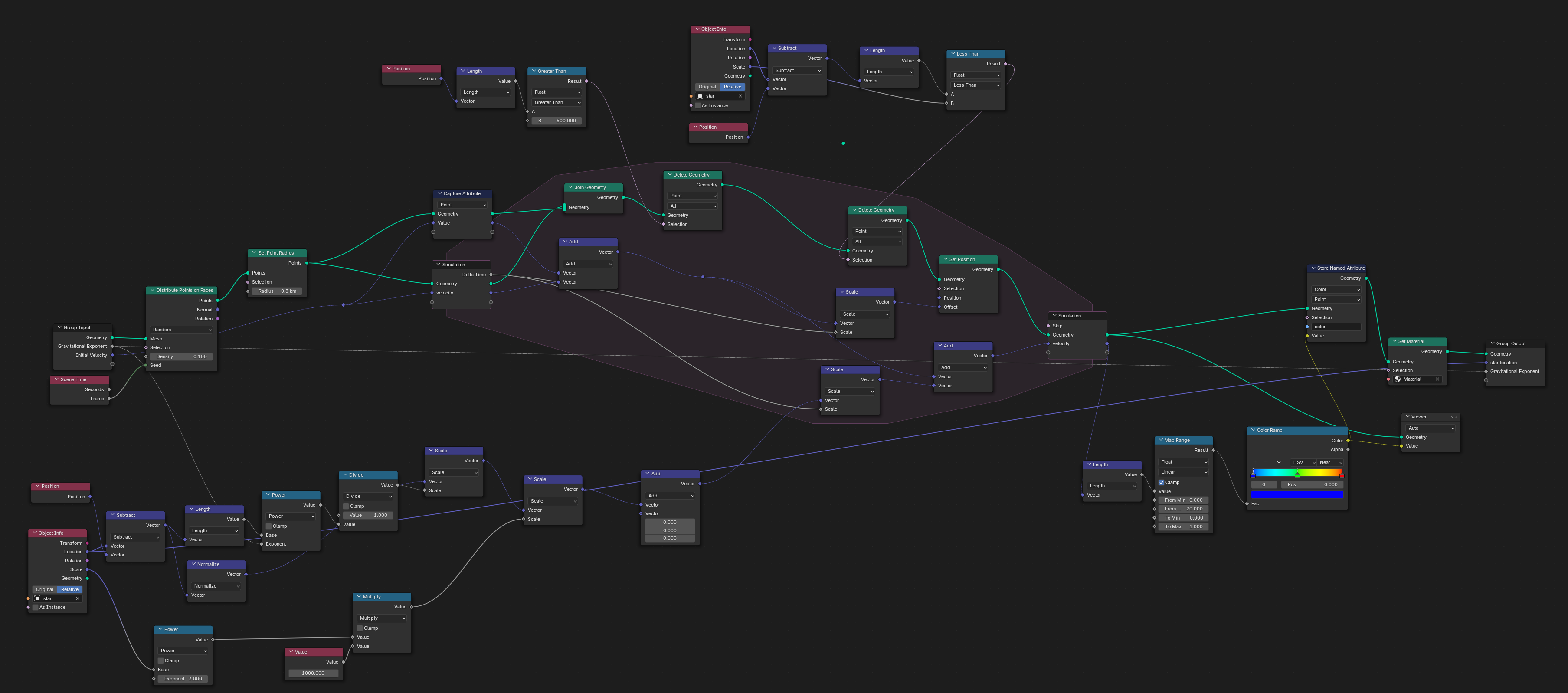
This graph calculates the $\frac{1}{r^2}$ factor by getting the position of an external attractive object, and then calculating the distance between each point in the geometry (these points are randomly generated each frame) we can simulate the effect of gravitation on these points. The $\frac{1}{r^2}$ nature of this law arises because of the 3 dimensional geometry that we live and compute in. This law gives rise to various orbits that are all in the family of conic sections or intersections of a plane with a cone. For orbits below a certain energy, the orbit shape is an ellipse shown below.

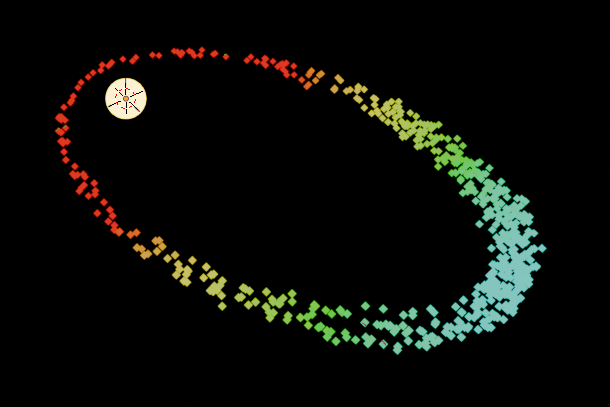
Changing the initial velocity changes the overall energy of the orbit, and the shape of the ellipse as shown in the video below:

The geometry nodes implementation allows us to change anything about this simulation including the number of points, the initial velocity (shown above), the size of the central star, the location of the central star, and the exponent of the law of gravitation. Changing this from the physical 2, to 1.9 gave rise to this video.